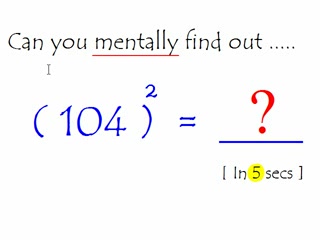ឥឡូវនេះចូរអ្នកធ្វើការគណនាលេខ (១០២)២ ដោយមិនប្រើម៉ាស៊ីនគិតលេខ។ តើអ្នករកឃើញចម្លើយដោយប្រើប្រាស់រយៈពេលប៉ុន្មានវិនាទី ឬនាទី? ប្រហែលជាប្រើរយៈពេលមិនតិចជាង៣០វិនាទីទេ។ ថ្ងៃនេះគំនិត សូមលើកយកវិធីមួយដែលអាចឲ្យអ្នកធ្វើការគណនាចំនួនស្វ័យគុណ២ (ចំនួនលេខខិតជិត១០០) ដោយប្រើរយៈពេលតិចជាង៥វិនាទី។
ដើម្បីធ្វើអោយមិត្តអ្នកអានងាយស្រួលយល់នោះ គំនិតនឹងលើកយកឧទាហរណ៍ ២ទៅ ៣ដើម្បីយកមកបង្ហាញក្នុងការធ្វើប្រមាណវិធីនេះ។ អញ្ចឹងសូមអ្នកទាំងអស់គ្នាត្រៀម ប៊ិច និងក្រដាសឲ្យហើយ ដើម្បីធ្វើការកត់ត្រានូវវិធី និងរៀនធ្វើតាម។
ឧទាហរណ៍យើងធ្វើការគណនា (១០៧)២=?៖ យើងយកលេខ១០០គឺជាគោល ហើយនៅក្នុងលំហាត់នេះ គឺយើងមាន១០៧ ដែលនាំអោយយើងបាន ១០៧-១០០=៧។ ដូចនេះយើងយក៧ដែលទទួលបានមកបូកបន្ថែមនឹងចំនួនដើម យើងបាន ១០៧+៧=១១៤។ ចំនួនស្វ័យគុណនឹង២ នៃចំនួនខិតជិត១០០(ចំនួនច្រើនជាង១០០) គឺមានចំនួន៥ខ្ទង់។ ពេលនេះយើងទទួលបាន១១៤ដែលមានចំនួន៣ខ្ទង់។ ដូចនេះសម្រាប់២ខ្ទង់បន្ទាប់ទៀត គឺយើងធ្វើការបំពេញបន្ថែមដោយយកចំនួនដែលយើងទទួលបានពីការដកនឹង១០០(១០៧-១០០=៧) ស្វ័យគុណនឹង២ គឺ (៧)២=៤៩។ ដូចនេះលទ្ធផលចុងក្រោយដែលយើងទទួលបានគឺ ១១៤៤៩។
ឧទាហរណ៍ទី២ គណនា (១១១)២=?៖ ក្នុងលំហាត់នេះ គឺយើងយក ១១១-១០០=១១។ ដូចនេះយកលទ្ធផលដែលទទួលបានទៅបូកនឹងចំនួនដើម ១១១+១១=១២២។ នៅសល់២ខ្ទង់ខាងក្រោយទៀត ដែលយើងត្រូវអនុវត្តតាមវិធីនៅក្នុងឧទាហរណ៍ទី១ គឺយក ១១ ធ្វើស្វ័យគុណនឹង២ គឺ (១១)២=១២១។ អ្វីដែលប្លែកពីឧទាហរណ៍មុននោះ គឺយើងទទួលបានលទ្ធផល១២១ ដែលមានដល់ទៅ៣ខ្ទង់។ ដូចនេះដើម្បីដោះស្រាយបញ្ហានេះ គឺយើងយកលេខខ្ទង់ទី១ នៃចំនួន ១២១ ទៅបូកបន្ថែមនឹងចំនួនដែលយើងរកឃើញដំបូង(១២២) យើងទទួលបាន ១២២+១=១២៣។ រីឯលេខពីរខ្ទង់ដែលស្ថិតនៅក្រោយចំនួន១២១ គឺលេខ ២១នោះ គឺយើងយកទៅបន្ថែម ពីខាងក្រោយ ១២៣ ដែលធ្វើអោយទទួលបានលទ្ធផលចុងក្រោយគឺ ១២៣២១។
ឧទាហរណ៍ទី៣ គណនា (៩៦)២=?៖ នៅក្នុងលំហាត់នេះគឺវាមានលេខតិចជាង១០០ ប៉ុន្តែវិធីគណនាគឺរក្សានៅដដែល គឺយើងយក ៩៦-១០០= -៤។ បន្ទាប់មកយើងយកលទ្ធផលដែលទទួលបាន យកទៅបូកនឹងលទ្ធផលដើម គឺ ៩៦-៤=៩២។ នៅសល់២ខ្ទង់ខាងក្រោយដែលត្រូវបំពេញបន្ថែមគឺយើងនៅតែអនុវត្តតាមវិធីដូចដើមដោយយក (-៤)២=១៦។ ដូចនេះលទ្ធផលចុងក្រោយយើងទទួលបាន ៩២១៦។
តើអ្នកអាចអនុវត្តតាមវិធីនេះហើយឬនៅ ប្រសិនបើមានចម្ងល់អ្វី ប្រិយមិត្តអាចសួរគំនិតបានគ្រប់ពេល។ J
